




Next: Standard Eigenvalue and Singular
Up: Driver Routines
Previous: Linear Least Squares (LLS)
Contents
Index
Generalized Linear Least Squares (LSE and GLM) Problems
Driver routines are provided for two types of generalized linear least squares
problems.
The first is
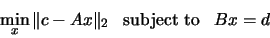 |
(2.2) |
where 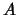 is an
is an 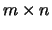 matrix and
matrix and 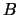 is a
is a 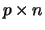 matrix,
matrix,
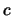 is a given
is a given 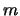 -vector, and
-vector, and 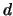 is a given
is a given 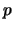 -vector,
with
-vector,
with
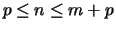 .
This is
called a linear equality-constrained least squares problem (LSE).
The routine LA_GGLSE
solves this problem using the generalized
.
This is
called a linear equality-constrained least squares problem (LSE).
The routine LA_GGLSE
solves this problem using the generalized 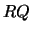 (GRQ) factorization,
on the
assumptions that
(GRQ) factorization,
on the
assumptions that  has full row rank
has full row rank 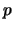 and
the matrix
and
the matrix
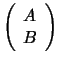 has full column rank
has full column rank  .
Under these assumptions, the problem LSE has a unique solution.
.
Under these assumptions, the problem LSE has a unique solution.
The second generalized linear least squares problem is
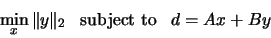 |
(2.3) |
where 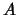 is an
is an 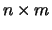 matrix,
matrix, 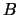 is an
is an 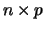 matrix,
and
matrix,
and 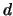 is a given
is a given  -vector,
with
-vector,
with
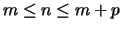 .
This is sometimes called a general (Gauss-Markov) linear model problem (GLM).
When
.
This is sometimes called a general (Gauss-Markov) linear model problem (GLM).
When 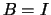 , the identity matrix, the problem reduces to an ordinary linear least squares problem.
When
, the identity matrix, the problem reduces to an ordinary linear least squares problem.
When 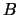 is square and nonsingular, the GLM problem is equivalent to the
weighted linear least squares problem:
is square and nonsingular, the GLM problem is equivalent to the
weighted linear least squares problem:
The routine LA_GGGLM
solves this problem using the generalized 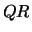 (GQR)
factorization,
on the
assumptions that
(GQR)
factorization,
on the
assumptions that 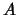 has full column rank
has full column rank 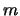 and the
matrix
and the
matrix 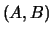 has full row rank
has full row rank  . Under these assumptions, the
problem is always consistent, and there are unique solutions
. Under these assumptions, the
problem is always consistent, and there are unique solutions  and
and 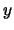 .
The driver routines for generalized linear least squares problems are listed
in Table 2.4.
.
The driver routines for generalized linear least squares problems are listed
in Table 2.4.
Table 2.4:
Driver routines for generalized linear least squares problems
| Operation |
real/complex |
| solve LSE problem using GRQ |
LA_GGLSE |
| solve GLM problem using GQR |
LA_GGGLM |





Next: Standard Eigenvalue and Singular
Up: Driver Routines
Previous: Linear Least Squares (LLS)
Contents
Index
Susan Blackford
2001-08-19
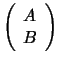 has full column rank
has full column rank