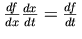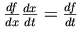 .
.
Overview: Mathematical Markup Language (MathML) Version 2.0
Previous: 1 Introduction
Next: 3 Presentation Markup
2 MathML Fundamentals
2.1 MathML Overview
2.1.1 Taxonomy of MathML Elements
2.1.2 Presentation Markup
2.1.3 Content Markup
2.1.4 Mixing Presentation and Content
2.2 MathML in a Document
2.3 Some MathML Examples
2.3.1 Presentation Examples
2.3.2 Content Examples
2.3.3 Mixed Markup Examples
2.4 MathML Syntax and Grammar
2.4.1 MathML Syntax and Grammar
2.4.2 An XML Syntax Primer
2.4.3 Children versus Arguments
2.4.4 MathML Attribute Values
2.4.5 Attributes Shared by all MathML Elements
2.4.6 Collapsing Whitespace in Input
This chapter introduces the basic ideas of MathML. The first section describes the overall design of MathML. The second section presents a number of motivating examples, to give the reader something concrete to refer to while reading subsequent chapters of the MathML specification. The final section describes basic features of the MathML syntax and grammar, which apply to all MathML markup. In particular, Section 2.4 [MathML Syntax and Grammar] should be read before Chapter 3 [Presentation Markup], Chapter 4 [Content Markup] and Chapter 5 [Combining Presentation and Content Markup].
A fundamental challenge in defining a markup language for mathematics on the Web is reconciling the need to encode both the presentation of a mathematical notation and the content of the mathematical idea or object which it represents.
The relationship between a mathematical notation and a mathematical idea
is subtle and deep. On a formal level, the results of mathematical logic
raise unsettling questions about the correspondence between systems of
symbolic logic and the phenomena they model. At a more intuitive level,
anyone who uses mathematical notation knows the difference that a good
choice of notation can make; the symbolic structure of the notation
suggests the logical structure. For example, the Leibniz notation for
derivatives `suggests' the chain rule of calculus through the
symbolic cancellation of fractions: 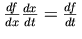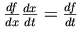 .
.
Mathematicians and teachers intuitively understand this very well; part of their expertise lies in choosing notation that emphasizes key aspects of a problem while hiding or diminishing extraneous aspects. It is commonplace in mathematics and science to write one thing when strictly technically something else is meant, because long experience shows this actually communicates the idea better at some higher level than rigorous detail.
In many other settings, though, mathematical notation is used to encode the full, precise meaning of a mathematical object. Mathematical notation is capable of prodigious rigor, and when used carefully, it can be virtually free of ambiguity. Moreover, it is precisely this lack of ambiguity which makes it possible to describe mathematical objects so that they can be used by software applications such as computer algebra systems and voice renderers. In situations where such inter-application communication is of paramount importance, the nuances of visual presentation generally play a minimal role.
MathML allows authors to encode both the notation which represents a mathematical object and the mathematical structure of the object itself. Moreover, authors can mix both kinds of encoding in order to specify both the presentation and content of a mathematical idea. The remainder of this section gives a basic overview of how MathML can be used in each of these ways.
All MathML elements fall into one of three categories: presentation elements, content elements and interface elements. Each of these categories is described in detail in Chapter 3 [Presentation Markup], Chapter 4 [Content Markup] and Chapter 7 [The MathML Interface], respectively.
Presentation elements describe mathematical notation's visually oriented
two-dimensional structure. Typical examples are the
mrow
element, which is usually employed to indicate a
horizontal row of pieces of expressions, and the
msup element, which is used to mark up a base
expression and a superscript to it. As a general rule, each presentation
element corresponds to a single kind of notational `schema'
such as a row, a superscript, a subscript, an underscript and so on.
Any formula is made by putting together parts which ultimately can
be analyzed down to the simplest items such as digits, letters, or
other symbol characters.
Although the previous paragraph was concerned with the display aspect of mathematical notation, and hence with presentation markup, the same observation about decomposition applies equally well to abstract mathematical objects, and hence to content markup. For example, in the context of content markup a superscript would typically be denoted by an exponentiation operation that would require two operands: a `base' and an `exponent'. This is no coincidence, since as a general rule, mathematical notation's layout closely follows the logical structure of the underlying mathematical objects.
The recursive nature of mathematical objects and notation is strongly reflected in MathML markup. In use, most presentation or content elements contain some number of other MathML elements corresponding to the constituent pieces out of which the original object is recursively built. The original schema is commonly called the parent schema, and the constituent pieces are called child schemata. More generally, MathML expressions can be regarded as trees, where each node corresponds to a MathML element, the branches under a `parent' node correspond to its `children', and the leaves in the tree correspond to atomic notation or content units such as numbers, characters, etc.
Most leaf nodes in a MathML expression tree are either canonically
empty elements with no bodies, or token elements.
Canonically empty elements represent symbols directly in MathML, for
example, the content element
<plus/> does
this. MathML token elements are the only MathML elements permitted to
contain MathML character data. MathML character data consists of
Unicode characters with the infrequent addition of special
character constructions done with the
mglyph
element. A third kind of leaf node
permitted in MathML is the
annotation element,
which is used to hold data which is not in MathML format.
The most important presentation token elements are
mi,
mn and
mo for representing identifiers, numbers and operators
respectively. Typically a renderer will employ slightly different
typesetting styles for each of these kinds of character data: numbers are
usually in upright font, identifiers in italics, and operators have extra
space around them. In content markup, there are only three tokens,
ci,
cn and
csymbol, for identifiers, numbers and new symbols
introduced in the document itself, respectively. In content markup,
separate elements are provided for commonly used functions and
operators. The
apply element is provided for
user-defined extensions to the base set.
In terms of markup, most MathML elements are denoted by a
start tag and an end tag, which enclose the
markup for their contents. In the case of tokens, the content is
character data, and in most other cases, the content is the markup for
child elements. Elements in a third category, called canonically empty
elements, do not require any contents, and are denoted by a single tag of
the form <name/>. An example of this kind of
markup is <plus/> in content markup.
Let us take the very simple example of (a + b)2, and we can now see how the principles discussed above play out in practice. One form of presentation markup for this example is:
<mrow>
<msup>
<mfenced>
<mrow>
<mi>a</mi>
<mo>+</mo>
<mi>b</mi>
</mrow>
</mfenced>
<mn>2</mn>
</msup>
</mrow>
This example demonstrates a number of presentation elements. The first
element, one that is used a great deal is
mrow.
This element is used to denote a row of horizontally aligned material. The
material contained between the <mrow> and </mrow> tags is considered to be an argument to the mrow element. Thus the whole expression here is
contained in an mrow element. As previously noted,
almost all mathematical expressions decompose into subexpressions. These
subexpressions can, in turn, also be contained in an mrow element. For example, a + b is also contained in an
mrow.
The
mfenced element is used to provide fences
(braces, brackets, and parentheses) around formula material. It defaults
to using parentheses.
Note the use of the
mi element for displaying
the variables a and b and the
mo element for
marking the + operator.
The
msup element is for expressions involving
superscripts and takes two arguments, in order, the base expression (here,
(a+b)) and the exponent expression (here, 2).
The content markup for the same example is:
<mrow>
<apply>
<power/>
<apply>
<plus/>
<ci>a</ci>
<ci>b</ci>
</apply>
<cn>2</cn>
</apply>
</mrow>
Here, the
apply content element means apply an
operation to an expression. In this example, the power element (for exponentiation), which requires no
body, and the similar
plus element (for addition)
are both applied. Observe that both operators take two
arguments, the order being particularly significant in the case of the
power operator. But the order of the children is crucial in the use
of the apply since the first child, the operator,
takes as argument list the remaining ones.
Note the use of the
ci element to mark up the
variables a and b, and the
cn element to mark up
the number 2.
MathML presentation markup consists of about 30 elements which accept
over 50 attributes. Most of the elements correspond to layout
schemata, which contain other presentation elements. Each layout
schema corresponds to a two-dimensional notational device, such as a
superscript or subscript, fraction or table. In addition, there are the
presentation token elements
mi,
mo and
mn introduced above, as
well as several other less commonly used token elements. The remaining few
presentation elements are empty elements, and are used mostly in connection
with alignment.
The layout schemata fall into several classes. One group of
elements is concerned with scripts, and contains elements such as
msub,
munder,
and mmultiscripts. Another group focuses on
more general layout and includes mrow, mstyle, and mfrac. A third group deals with tables.
The maction element is in a category by
itself, and allows coding of various kinds of actions on notation,
such as occur in an expression which toggles between two pieces of
notation.
An important feature of many layout schemata is that the order of child
schemata is significant. For example, the first child of an
mfrac element is the numerator and the second child is
the denominator. Since the order of child schemata is not enforced at the
XML level by the MathML DTD, the information added by ordering is only
available to a MathML processor, as opposed to a generic XML processor.
When we want to emphasize that a MathML element such as
mfrac requires children in a specific order, we will
refer to them as arguments, and think of the
mfrac element as a notational
`constructor'.
Content markup consists of about 120 elements accepting roughly a dozen
attributes. The majority of these elements are empty elements corresponding
to a wide variety of operators, relations and named functions. Examples of
this sort include
partialdiff,
leq and
tan. Others such as
matrix and
set are used to
encode various mathematical data types, and a third, important category of
content elements such as
apply are used to apply
operations to expressions and also to make new mathematical objects from
others.
The
apply element is perhaps the single most
important content element. It is used to apply a function or operation to a
collection of arguments. The positions of the child schemata are again
significant, with the first child denoting the function to be applied, and
the remaining children denoting the arguments of the function in
order. Note that the apply construct always uses
prefix notation, like the programming language LISP. In particular, even
binary operations such as subtraction are marked up by applying a prefix
subtraction operator to two arguments. For example, a -
b would be marked up as
<mrow> <apply> <minus/> <ci>a</ci> <ci>b</ci> </apply> </mrow>
A number of functions and operations require one or more quantifiers to
be well-defined. For example, in addition to an integrand, a definite
integral must specify the limits of integration and the bound variable. For
this reason, there are several qualifier schemata such as
bvar and
lowlimit. They are
used with operators such as
diff and
int.
The
declare construct is especially important
for content markup that might be evaluated by a computer algebra system.
The declare element provides a basic assignment
mechanism, where a variable can be declared to be of a certain type, with a
certain value.
In both the presentation and content markup examples, mathematical expressions are recursively decomposed into nested, simpler MathML elements specifying each stage of the decomposition. The examples in the following sections illustrate this with more complex expressions.
Different kinds of markup will be found most appropriate for different kinds of tasks. Documents written before the World Wide Web became important were most often intended only for visual communication of information, so that legacy data is probably best translated into pure presentation markup, since semantic information about what the author meant can only be guessed at heuristically. By contrast, some mathematical applications and pedagogically-oriented authoring tools will likely choose to be entirely content-based. The majority of applications fall somewhere in between these extremes. For these applications, the most appropriate markup is a mixture of both presentation and content markup.
The rules for mixing presentation and content markup derive from the general principle that mixed content should only be allowed in places where it makes sense. For content markup embedded in presentation markup this basically means that any content fragments should be semantically meaningful, and should not require additional arguments or quantifiers to be fully specified. For presentation markup embedded in content markup, this usually means that presentation markup must be contained in a content token element, so that it will be treated as an indivisible notational unit used as a variable or function name.
Another option is to use a
semantics element.
The semantics element is used to bind MathML
expressions to various kinds of annotations. One common use for the semantics element is to bind a piece of content markup
to some presentation markup as a semantic annotation. In this way, an
author can specify a non-standard notation to be used when displaying a
particular content expression. Another use of the semantics element is to bind some other kind of
semantic specification, such as an OpenMath expression, to a MathML
expression. In this way, the semantics element can
be used to extend the scope of MathML content markup.
The discussion above has actually been of fragmentary formulas outside the context of any document. To be more specific let us look at what corresponds to a programming language's "Hello World!" example. We shall provide more complete code for an XHTML 1.0 document containing the square of a sum of two variables mentioned above. It would be
<html xmlns="http://www.w3.org/1999/xhtml" lang="en" xml:lang="en">
<head>
<title>MathML's Hello Square</title>
</head>
<body>
<p> This is a perfect square:</p>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mrow>
<msup>
<mfenced>
<mrow>
<mi>a</mi>
<mo>+</mo>
<mi>b</mi>
</mrow>
</mfenced>
<mn>2</mn>
</msup>
</mrow>
</math>
</body>
</html>
Here we have the normal structure of an XHTML document. It begins
with the start tag <html> embellished with an
XML namespace declaration and language assertions. A head element contains a title as is customary.
Then the <body> beginning also has a namespace
declaration of an abbreviative prefix letter m
to be used for the standard MathML namespace. Next comes a simple
paragraph. Finally we get the math element
which also has a namespace association declared. Inside the math element is MathML markup as we are beginning
to be used to it. The reasons why one might have to do a more complex
namespace declaration for MathML are explained in Chapter 7 [The MathML Interface]; they have to do with present-day limitations in some XML
handling, that may be expected to go away.
For the next level of technical detail concerning such matters
as !DOCTYPE statements and the like, see the
discussion in Chapter 7 [The MathML Interface].
We continue below to display examples in the form of fragments of
MathML markup such as would appear inside math
elements in real documents. For the sake of clearer exposition of
principles, the examples in Chapters 3, 4, 5 and 6 follow this form of
giving examples as MathML fragments.
Notation: x2 + 4x + 4 = 0.
Markup:
<mrow>
<mrow>
<msup>
<mi>x</mi>
<mn>2</mn>
</msup>
<mo>+</mo>
<mrow>
<mn>4</mn>
<mo>⁢</mo>
<mi>x</mi>
</mrow>
<mo>+</mo>
<mn>4</mn>
</mrow>
<mo>=</mo>
<mn>0</mn>
</mrow>
Note the use of nested mrow elements to denote terms, for
example, the left-hand side of the equation functioning as an operand
of `='. Marking terms greatly facilitates spacing for
visual rendering, voice rendering, and line breaking. The InvisibleTimes MathML character entity is used here
to indicate to a renderer that there are special spacing rules between
the 4 and the x, and that the 4 and the x should not be broken onto
separate lines. In fact, this use of an entity which was introduced
in MathML 1.0 is no longer the way that is preferred. Ultimately all
ordinary character data is given by Unicode values. However, although
a character for ⁢ is expected in
Unicode 3.2, and there is a suggested code point under
consideration in a Unicode amendment, there is no Unicode 3.0
character to be used at present. We could use the expected numerical
character reference ࠎ but for clarity we will continue to
use entity references in these examples. The situation is explicitly
discussed in Section 3.2 [Token Elements] and in Chapter 6 [Characters, Entities and Fonts].
Notation:
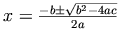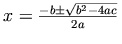 .
.
Markup:
<mrow>
<mi>x</mi>
<mo>=</mo>
<mfrac>
<mrow>
<mrow>
<mo>-</mo>
<mi>b</mi>
</mrow>
<mo>±</mo>
<msqrt>
<mrow>
<msup>
<mi>b</mi>
<mn>2</mn>
</msup>
<mo>-</mo>
<mrow>
<mn>4</mn>
<mo>⁢</mo>
<mi>a</mi>
<mo>⁢</mo>
<mi>c</mi>
</mrow>
</mrow>
</msqrt>
</mrow>
<mrow>
<mn>2</mn>
<mo>⁢</mo>
<mi>a</mi>
</mrow>
</mfrac>
</mrow>
The
mfrac and
msqrt
elements are used for generating fractions
and square roots, respectively.
Notice that the `plus or minus' sign is given by a special
entity name ±, though in this case there
already is a Unicode character �B1;.
MathML provides a very comprehensive list of character names for
mathematical symbols. In addition to the mathematical symbols needed for
screen and print rendering, MathML provides symbols to facilitate audio
rendering. For audio rendering, it is important to be able to
automatically determine whether
<mrow>
<mi>z</mi>
<mfenced>
<mrow>
<mi>x</mi>
<mo>+</mo>
<mi>y</mi>
</mrow>
</mfenced>
</mrow>
should be read as `z times the quantity x plus
y' or `z of x plus y'. The
characters ⁢ (U+2062) and ⁡ (U+2061) provide a way for authors to
directly encode the distinction for audio renderers. For instance, in
the first case ⁢ (U+2062) should
be inserted after the line containing the z. MathML also
introduces entities like ⅆ (U+2146)
representing a `differential d', which renders with slightly
different spacing in print and can be rendered as `d' or
`with respect to' in speech. Unless content tags, or some
other mechanism, are used to eliminate the ambiguity, authors should
always use these characters here referred to as entities, in order to
make their documents more accessible.
Notation:
![A=\left[\begin{array}{cc} x & y \\ z & w \end{array}\right]](http://www.w3.org/TR/2001/REC-MathML2-20010221/image/f2008.gif) .
.
Markup:
<mrow>
<mi>A</mi>
<mo>=</mo>
<mfenced open="[" close="]">
<mtable>
<mtr>
<mtd><mi>x</mi></mtd>
<mtd><mi>y</mi></mtd>
</mtr>
<mtr>
<mtd><mi>z</mi></mtd>
<mtd><mi>w</mi></mtd>
</mtr>
</mtable>
</mfenced>
</mrow>
The mtable element denotes that a
MathML table is being created. The mtr
specifies a row of the table and the mtd
element holds the data for an element of a row. Most elements have a
number of attributes that control the details of their screen and
print rendering. For example, there are several attributes for the mfenced element that controls what delimiters
should be used at the beginning and the end of the grouped expression
above. The attributes for operator elements given using <mo> are set to default values determined by a
dictionary. For the suggested MathML operator dictionary, see Appendix F [Operator Dictionary].
Notation: x2 + 4x + 4 = 0.
Markup:
<mrow>
<apply>
<eq/>
<apply>
<plus/>
<apply>
<power/>
<ci>x</ci>
<cn>2</cn>
</apply>
<apply>
<times/>
<cn>4</cn>
<ci>x</ci>
</apply>
<cn>4</cn>
</apply>
<cn>0</cn>
</apply>
</mrow>
Note that the apply element is used for
relations, operators and functions.
Notation:
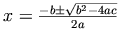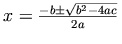 .
.
Markup:
<mrow>
<apply>
<eq/>
<ci>x</ci>
<apply>
<divide/>
<apply>
<mo>±</mo>
<apply>
<minus/>
<ci>b</ci>
</apply>
<apply>
<root/>
<apply>
<minus/>
<apply>
<power/>
<ci>b</ci>
<cn>2</cn>
</apply>
<apply>
<times/>
<cn>4</cn>
<ci>a</ci>
<ci>c</ci>
</apply>
</apply>
<cn>2</cn>
</apply>
</apply>
<apply>
<times/>
<cn>2</cn>
<ci>a</ci>
</apply>
</apply>
</apply>
</mrow>
MathML content markup does not directly contain an element for the
`plus or minus' operation. Therefore, we use the mo element to declare that we want the presentation
markup for this operator to act as a content operator. This is a simple
example of how presentation and content markup can be mixed to extend
content markup.
Notation:
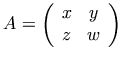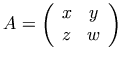 .
.
Markup:
<mrow>
<apply>
<eq/>
<ci>A</ci>
<matrix>
<matrixrow>
<ci>x</ci>
<ci>y</ci>
</matrixrow>
<matrixrow>
<ci>z</ci>
<ci>w</ci>
</matrixrow>
</matrix>
</apply>
</mrow>
Here we have used the matrix element, and the
matrixrow element to wrap the entries in a row of
the matrix. Note that, by default, the rendering of the content
element matrix includes enclosing parentheses,
so we need not directly encode them. This is quite different from the
presentation element mtable which may or may
not refer to a matrix, and hence requires explicit encoding of
parentheses if they are desired.
Notation:
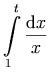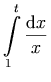 .
.
Markup:
<mrow>
<semantics>
<mrow>
<msubsup>
<mo>∫</mo>
<mn>1</mn>
<mi>t</mi>
</msubsup>
<mfrac>
<mrow>
<mo>ⅆ</mo>
<mi>x</mi>
</mrow>
<mi>x</mi>
</mfrac>
</mrow>
<annotation-xml encoding="MathML-Content">
<apply>
<int/>
<bvar><ci>x</ci></bvar>
<lowlimit><cn>1</cn></lowlimit>
<uplimit><ci>t</ci></uplimit>
<apply>
<divide/>
<cn>1</cn>
<ci>x</ci>
</apply>
</apply>
</annotation-xml>
</semantics>
</mrow>
In this example, we use the semantics
element to provide a MathML content expression to serve as a
`semantic annotation' for a presentation expression. In
the display markup, we have used the msubsup
element to attach a subscript and a superscript to an expression, in
this case the integral sign. We also used entities ∫ and ⅆ to specify the
integral and differential symbols.
The semantics element has as its first child
the expression being annotated, and the subsequent children are the
annotations. There is no restriction on the kind of annotation that
can be attached using the semantics element.
For example, one might give a TEX encoding, or computer algebra
input in an annotation. The type of annotation is specified by the encoding attribute and the annotation and annotation-xml elements.
Another common use of the semantics
element arises when one wants to use a content coding, and
provide a suggestion for its presentation. In such a case,
applied to the formula above we would have the markup:
<semantics>
<apply>
<int/>
<bvar><ci>x</ci></bvar>
<lowlimit><cn>1</cn></lowlimit>
<uplimit><ci>t</ci></uplimit>
<apply>
<divide/>
<cn>1</cn>
<ci>x</ci>
</apply>
</apply>
<annotation-xml encoding="MathML-Presentation">
<mrow>
<msubsup>
<mo>∫</mo>
<mn>1</mn>
<mi>t</mi>
</msubsup>
<mfrac>
<mrow>
<mo>ⅆ</mo>
<mi>x</mi>
</mrow>
<mi>x</mi>
</mfrac>
</mrow>
</annotation-xml>
</semantics>
This kind of annotation is useful when something other than the default rendering of the content encoding is desired. For example, by default, some renderers might layout the integrand something like `(1/x) dx'. Specifying that the integrand should by preference render as `dx/x' instead can be accomplished with the use of a MathML Presentation annotation as shown. Be aware, however, that renderers are not required to take into account information contained in annotations, and what use is made of them, if any, will depend on the renderer.
MathML is an application of [XML], or Extensible Markup Language, and as such its syntax is governed by the rules of XML syntax, and its grammar is in part specified by a DTD, or Document Type Definition. In other words, the details of using tags, attributes, entity references and so on are defined in the XML language specification, and the details about MathML element and attribute names, which elements can be nested inside each other, and so on are specified in the MathML DTD. This is in Appendix A [Parsing MathML].
The W3C in seeking to increase the flexibility of the use of XML for the Web, and to encourage modularization of applications built with XML, has found that the basic form of a DTD is not sufficiently flexible. Therefore, a W3C Working Group was created to develop a specification for XML Schemas [XMLSchemas], which are specification documents that will eventually supersede DTDs. MathML 2.0 is consciously designed so that mathematics may take advantage of the latest in the evolving Web technology. Thus, there is to be a schema for MathML. For further information on a MathML schema see Appendix A [Parsing MathML] and the MathML Home Page.
However, MathML also specifies some syntax and grammar rules in addition to the general rules it inherits as an XML application. These rules allow MathML to encode a great deal more information than would ordinarily be possible with pure XML, without introducing many more elements, and using a substantially more complex DTD or schema. A grammar for content markup expressions is given in Appendix B [Content Markup Validation Grammar]. Of course, one drawback to using MathML specific rules is that they are invisible to generic XML processors and validators.
There are basically two kinds of additional MathML grammar and syntax rules. One kind involves placing additional criteria on attribute values. For example, it is not possible in pure XML to require that an attribute value be a positive integer. The second kind of rule specifies more detailed restrictions on the child elements (for example on ordering) than are given in the DTD or even a schema. For example, it is not possible in XML to specify that the first child be interpreted one way, and the second in another.
The following sections discuss features both of XML syntax and grammar in general, and of MathML in particular. Throughout the remainder of the MathML specification, we will usually take care to distinguish between usage required by XML syntax and the MathML DTD (and schema) and usage required by MathML specific rules. However, we will frequently allude to `MathML errors' without identifying which part of the specification is being violated.
Since MathML is an application of XML, the MathML specification uses the
terminology of XML to describe it. Briefly, XML data is composed of Unicode
characters (which include ordinary ASCII characters), `entity
references' (informally called `entities') such as < which usually represent `extended
characters', and `elements' such as <mi
fontstyle="normal"> x </mi>.
An element quite often encloses other XML data called its
`content', or `body', between a `start
tag' (sometimes called a `begin tag') and an `end
tag', much as in HTML. There are also `empty elements'
such as <plus/>, whose start tag ends with
/> to indicate that the element has no content or end
tag. The start tag can contain named parameters called
`attributes', such as fontstyle="normal" in the
example above. For further details on XML, consult the XML specification
[XML].
As XML is case-sensitive, MathML element and attribute names are case-sensitive. For reasons of legibility, the MathML specification defines them almost all in lowercase.
In formal discussions of XML markup, a distinction is maintained
between an element, such as an mrow element,
and the tags <mrow> and </mrow> marking it. What is between the <mrow> start tag and the </mrow> end tag is the content, or body, of the mrow element. An `empty element'
such as none is defined to have no body, and
so has a single tag of the form <none/>.
Usually, the distinction between elements and tags will not be so
finely drawn in this specification. For instance, we will sometimes
refer to the <mrow> and <none/> elements, really meaning the elements whose
tags these are, in order that references to elements are visually
distinguishable from references to attributes. However, the words
`element' and `tag' themselves will be used
strictly in accordance with XML terminology.
Many MathML elements require a specific number of child elements or attach additional meanings to children in certain positions. As noted above, these kinds of requirements are MathML specific, and cannot be given entirely using XML syntax and grammar. When the children of a given MathML element are subject to these kinds of additional conditions, we will often refer to them as arguments instead of merely as children, in order to emphasize their MathML specific usage. Note that, especially in Chapter 3 [Presentation Markup], the term `argument' is usually used in this technical sense, unless otherwise noted, and therefore refers to a child element.
In the detailed discussions of element syntax given with each element throughout the MathML specification, the number of required arguments and their order is implicitly indicated by giving names for the arguments at various positions. This information is also given for presentation elements in the table of argument requirements in Section 3.1.3 [Required Arguments], and for content elements in Appendix B [Content Markup Validation Grammar].
A few elements have other requirements on the number or type of arguments. These additional requirements are described together with the individual elements.
According to the XML language specification, attributes given to elements must have one of the forms
attribute-name = "value"
or
attribute-name = 'value'
where whitespace around the '=' is optional.
Attribute names are generally shown in a monospaced font within descriptive text in this
specification, just as the monospaced font is used
for examples.
An attribute's value, which in general in MathML can be a string of
arbitrary characters, must be surrounded by a pair of either double quotes
(") or single quotes ('). The kind of quotes
not used to surround the value may be included within it.
MathML uses a more complicated syntax for attribute values than the generic XML syntax required by the MathML DTD. These additional rules are intended for use by MathML applications, and it is a MathML error to violate them, though they cannot be enforced by XML processing. The MathML syntax of each attribute value is specified in the table of attributes provided with the description of each element, using a notation described below. When MathML applications process attribute values, whitespace is ignored except to separate letter and digit sequences into individual words or numbers. Attribute values may contain any MathML characters listed in Section 6.2 [MathML Characters] permitted by the syntax restrictions for an attribute. Character data can be included directly in attribute values, or by using entity references as described in Section 6.2.1 [Unicode Character Data].
In particular, the characters ", ',
& and < can be included in MathML
attribute values (when permitted by the attribute value syntax) using the
entity references ", ',
& and <, respectively.
The MathML DTD provided in Appendix A [Parsing MathML] declares most
attribute value types as CDATA strings. This permits increased
interoperability with existing SGML and XML software and allows extension
to the lists of predefined values. Similar sorts of considerations apply
with XML schemas.
To describe the MathML-specific syntax of permissible attribute values, the following conventions and notations are used for most attributes in the present document.
| Notation | What it matches |
|---|---|
| number | decimal integer or rational number (a string of digits with one decimal point), optionally starting with '-' |
| unsigned-number | decimal integer or real number, no sign |
| integer | decimal integer, optionally starting with '-' |
| positive-integer | decimal integer, unsigned, not 0 |
| string | arbitrary string (always the entire attribute value) |
| character | single non-whitespace character, or MathML entity reference; whitespace separation is optional |
| #rrggbb | RGB color value; the three pairs of hexadecimal digits in the example #5599dd define proportions of red, green and blue on a scale of x00 through xFF, which gives a strong sky blue. |
| h-unit | unit of horizontal length (allowable units are listed below) |
| v-unit | unit of vertical length (allowable units are listed below) |
| css-fontfamily | explained in the CSS subsection below |
| css-color-name | explained in the CSS subsection below |
| other italicized words | explained in the text for each attribute |
| form + | one or more instances of 'form' |
| form * | zero or more instances of 'form' |
| f1 f2 ... fn | one instance of each form, in sequence, perhaps separated by whitespace |
| f1 | f2 | ... | fn | any one of the specified forms |
| [ form ] | an optional instance of 'form' |
| ( form ) | same as form |
| word in plain text | that word, literally present in the attribute value (unless it is obviously part of an explanatory phrase) |
| quoted symbol | that symbol, literally present in attribute value (e.g. "+" or '+') |
The order of precedence of the syntax notation operators is, from highest to lowest precedence:
A string can contain arbitrary characters which are
specifiable within XML CDATA attribute values. See Chapter 6 [Characters, Entities and Fonts] for a discussion and complete listing of MathML
characters. No syntax rule in MathML includes a string
as only part of an attribute value, only as the entire value.
Adjacent keywords and numbers must be separated by whitespace in the
actual attribute values, except for unit identifiers (denoted by h-unit or v-unit syntax symbols)
following numbers. Whitespace is not otherwise required, but is permitted
between any of the tokens listed above, except (for compatibility with
CSS) immediately before unit identifiers, between the '-' signs and digits
of negative numbers, or between # or rrggbb and rgb.
Numerical attribute values for dimensions that should depend upon the
current font can be given in font-related units, or in named absolute units
(described in a separate subsection below). Horizontal dimensions are
conventionally given in em's, and vertical dimensions in
ex's, by immediately following a number by one of the unit
identifiers em or ex. For
example, the horizontal spacing around an operator such as `+'
is conventionally given in ems, though other units
can be used. Using font-related units is usually preferable to using
absolute units, since it allows renderings to grow or shrink in proportion
to the current font size.
For most numerical attributes, only those in a subset of the expressible values are sensible; values outside this subset are not errors, unless otherwise specified, but rather are rounded up or down (at the discretion of the renderer) to the closest value within the allowed subset. The set of allowed values may depend on the renderer, and is not specified by MathML.
If a numerical value within an attribute value syntax description is
declared to allow a minus sign ('-'), e.g. number or
integer, it is not a syntax error when one is
provided in cases where a negative value is not sensible. Instead, the
value should be handled by the processing application as described in the
preceding paragraph. An explicit plus sign ('+') is not allowed as part of
a numerical value except when it is specifically listed in the syntax (as a
quoted '+' or "+"), and its presence can change the meaning of the
attribute value (as documented with each attribute which permits it).
The symbols h-unit, v-unit, css-fontfamily,
and css-color-name are explained in the
following subsections.
Some attributes accept horizontal or vertical lengths as numbers
followed by a `unit identifier' (often just called a
`unit'). The syntax symbols h-unit and
v-unit refer to a unit for horizontal or vertical
length, respectively. The possible units and the lengths they refer to are
shown in the table below; they are the same for horizontal and vertical
lengths, but the syntax symbols are distinguished in attribute syntaxes as
a reminder of the direction each is used in.
The unit identifiers and meanings are taken from CSS. However, the syntax of numbers followed by unit identifiers in MathML is not identical to the syntax of length values with units in CSS style sheets, since numbers in CSS cannot end with decimal points, and are allowed to start with '+' signs.
The possible horizontal or vertical units in MathML are:
| Unit identifier | Unit description |
|---|---|
| em | em (font-relative unit traditionally used for horizontal lengths) |
| ex | ex (font-relative unit traditionally used for vertical lengths) |
| px | pixels, or pixel size of the current display |
| in | inches (1 inch = 2.54 centimeters) |
| cm | centimeters |
| mm | millimeters |
| pt | points (1 point = 1/72 inch) |
| pc | picas (1 pica = 12 points) |
| % | percentage of default value |
The typesetting units em and ex are defined in Appendix H [Glossary], and
discussed further under `Additional notes' below.
% is a `relative unit'; when an attribute
value is given as n% (for any numerical value n), the value being specified is the default value for
the property being controlled multiplied by n
divided by 100. The default value (or the way in which it is obtained, when
it is not constant) is listed in the table of attributes for each element,
and its meaning is described in the subsequent documentation about that
attribute. (The mpadded element has its own syntax
for % and does not allow it as a unit identifier.)
For consistency with CSS, length units in MathML are rarely
optional. When they are, the unit symbol is enclosed in square brackets in
the attribute syntax, following the number to which it applies,
e.g. number [ h-unit ]. The meaning of specifying no unit is
given in the documentation for each attribute; in general it is that the
number given is a multiplier for the default value of the attribute. (In
such cases, specifying the number nnn without a unit
is equivalent to specifying the number nnn times 100
followed by %. For example, <mo maxsize="2"> (
</mo> is equivalent to <mo maxsize="200%"> (
</mo>.)
As a special exception (also consistent with CSS), a numerical value equal to 0 need not be followed by a unit identifier even if the syntax specified here requires one. In such cases, the unit identifier (or lack of one) would not matter, since 0 times any unit is 0.
For most attributes, the typical unit which would be used to describe
them in typesetting is chosen as the one used in that attribute's default
value in this specification; when a specific default value is not given,
the typical unit is usually mentioned in the syntax table or in the
documentation for that attribute. The most common units are em
or ex. However, any unit can be used, unless otherwise
specified for a specific attribute.
Note that some attributes, e.g. framespacing
on a <mtable>,
can contain more than one numerical value, each followed by its own
unit.
It is conventional to use the font-relative unit ex mainly
for vertical lengths, and em mainly for horizontal lengths,
but this is not required. These units are relative to the font and font size
which would be used for rendering the element in whose attribute value they
are specified, which means they should be interpreted after
attributes such as fontfamily and fontsize are processed, if those occur on the same
element, since changing the current font or font size can change the length
of one of these units.
The definition of the length of each unit, but not the MathML syntax for
length values, is as specified in CSS, except that if a font provides
specific values for em and ex which differ from
the values defined by CSS (the font size and `x'-height
respectively), those values should be used.
Several MathML attributes, listed below, correspond closely to text rendering properties defined originally in [CSS1]. In MathML 1.01, the names and values of these attributes were aligned with the CSS Recommendation where possible. This was done so that renderers in CSS environments could query the environment for the corresponding property when determining the default values for the attributes.
Allowing style properties to be set both via MathML attributes and CSS style sheets has drawbacks. At a minimum, its confusing, and at worst, it leads to the meaning of equations being inadvertently changed by document-wide CSS changes. For these reasons, these attributes have been deprecated. In their place, MathML 2.0 introduces four new mathematical style attributes. These attributes use logical values to better capture the abstract categories of letter-like symbols used in math, and afford a much cleaner separation between MathML and CSS. See Section 3.2.2 [Mathematics style attributes common to token elements] for more details.
For reference, a table showing the correspondence of the deprecated MathML 1.01 style attribute with the CSS counterparts is given below:
| MathML attribute | CSS property | syntax symbol | MathML elements | refer to |
|---|---|---|---|---|
| fontsize | font-size | - | presentation tokens; mstyle |
Section 3.2.2 [Mathematics style attributes common to token elements] |
| fontweight | font-weight | - | presentation tokens; mstyle |
Section 3.2.2 [Mathematics style attributes common to token elements] |
| fontstyle | font-style | - | presentation tokens; mstyle |
Section 3.2.2 [Mathematics style attributes common to token elements] |
| fontfamily | font-family | css-fontfamily | presentation tokens; mstyle |
Section 3.2.2 [Mathematics style attributes common to token elements] |
| color | color | css-color-name | presentation tokens; mstyle |
Section 3.3.4 [Style Change (mstyle)] |
| background | background | css-color-name | mstyle |
Section 3.3.4 [Style Change (mstyle)] |
See also Section 2.4.5 [Attributes Shared by all MathML Elements] below for a discussion of the class, style and id attributes for use with style sheets.
CSS or analogous style sheets can specify changes to rendering
properties of selected MathML elements. Since rendering properties
can also changed by attributes on an element, or changed automatically
by the renderer, it is necessary to specify the order in which changes
from various sources occur. An example of automatic adjustment is what
happens for fontsize, as explained in the
discussion on scriptlevel in Section 3.3.4 [Style Change (mstyle)]. In the case of `absolute' changes,
i.e., setting a new property value independent of the old value (as
opposed to `relative' changes, such as increments or
multiplications by a factor), the absolute change performed last will
be the only absolute change which is effective, so the sources of
changes which should have the highest priority must be processed
last.
In the case of CSS, the order of processing of changes from various sources which affect one MathML element's rendering properties should be as follows:
(first changes; lowest priority)
fontsize in relation to scriptlevel mentioned above; such changes will usually
be implemented by the parent element itself before it passes a set of
rendering properties to this element(last changes; highest priority)
Note that the order of the changes derived from CSS style sheets is specified by CSS itself (this is the order specified by CSS2). The following rationale is related only to the issue of where in this pre-existing order the changes caused by explicit MathML attribute settings should be inserted.
Rationale: MathML rendering attributes are analogous to HTML rendering
attributes such as align, which the CSS section on
cascading order specifies should be processed with the same priority.
Furthermore, this choice of priority permits readers, by declaring certain
CSS styles as `important', to decide which of their style
preferences should override explicit attribute settings in MathML. Since
MathML expressions, whether composed of `presentation' or
`content' elements, are primarily intended to convey meaning,
with their `graphic design' (if any) intended mainly to aid in
that purpose but not to be essential in it, it is likely that readers will
often want their own style preferences to have priority; the main exception
will be when a rendering attribute is intended to alter the meaning
conveyed by an expression, which is generally discouraged in the
presentation attributes of MathML.
Default values for MathML attributes are in general given along with the detailed descriptions of specific elements in the text. Default values shown in plain text in the tables of attributes for an element are literal (unless they are obviously explanatory phrases), but when italicized are descriptions of how default values can be computed.
Default values described as inherited are taken from the
rendering environment, as described under mstyle,
or in some cases (described individually) from the values of other
attributes of surrounding elements, or from certain parts of those
values. The value used will always be one which could have been specified
explicitly, had it been known; it will never depend on the content or
attributes of the same element, only on its environment. (What it means
when used may, however, depend on those attributes or the content.)
Default values described as automatic should be computed by a MathML renderer in a way which will produce a high-quality rendering; how to do this is not usually specified by the MathML specification. The value computed will always be one which could have been specified explicitly, had it been known, but it will usually depend on the element content and possibly on the rendering environment.
Other italicized descriptions of default values which appear in the tables of attributes are explained for each attribute individually.
The single or double quotes which are required around attribute values in an XML start tag are not shown in the tables of attribute value syntax for each element, but are shown around example attribute values in the text.
Note that, in general, there is no value which can be given explicitly
for a MathML attribute which will simulate the effect of not specifying the
attribute at all for attributes which are inherited or
automatic. Giving the words `inherited' or
`automatic' explicitly will not work, and is not generally
allowed. Furthermore, even for presentation attributes for which a
specific default value is documented here, the mstyle element (Section 3.3.4 [Style Change (mstyle)]) can be
used to change this for the elements it contains. Therefore, the MathML DTD
declares most presentation attribute default values as #IMPLIED,
which prevents XML preprocessors from adding them with any specific default
value. This point of view is carried through to the MathML schema.
In an XML DTD, allowed attribute values can be declared as general strings, or they can be constrained in various ways, either by enumerating the possible values, or by declaring them to be certain special data types. The choice of an XML attribute type affects the extent to which validity checks can be performed using a DTD.
The MathML DTD specifies formal XML attribute types for all MathML
attributes, including enumerations of legitimate values in some cases. In
general, however, the MathML DTD is relatively permissive, frequently
declaring attribute values as strings; this is done to provide for
interoperability with SGML parsers while allowing multiple attributes on
one MathML element to accept the same values (such as true and false), and also to
allow extension to the lists of predefined values.
At the same time, even though an attribute value may be declared as a string in the DTD, only certain values are legitimate in MathML, as described above and in the rest of this specification. For example, many attributes expect numerical values. In the sections which follow, the allowed attribute values are described for each element. To determine when these constraints are actually enforced in the MathML DTD, consult Appendix A [Parsing MathML]. However, lack of enforcement of a requirement in the DTD does not imply that the requirement is not part of the MathML language itself, or that it will not be enforced by a particular MathML renderer. (See Section 7.2.2 [Handling of Errors] for a description of how MathML renderers should respond to MathML errors.)
Furthermore, the MathML DTD is provided for convenience; although it is intended to be fully compatible with the text of the specification, the text should be taken as definitive if there is a contradiction. (Any contradictions which may exist between various chapters of the text should be resolved by favoring Chapter 6 [Characters, Entities and Fonts] first, then Chapter 3 [Presentation Markup], Chapter 4 [Content Markup], then Section 2.4 [MathML Syntax and Grammar], and then other parts of the text.) For the MathML schema the situation will be the same: the published Recommendation text takes precedence. Though this is what is intended to happen, there is a practical difficulty. If the system processing the MathML uses a validating parser, whether it be based on a DTD or on a schema, the process will probably simply stop when it hits something held to be incorrect syntax, whether or not further MathML processing in full harmony with the specification would have processed the piece correctly.
In order to facilitate use with style sheet mechanisms such as
[XSLT] and [CSS2]
all MathML elements accept class, style, and id attributes in addition to the attributes described
specifically for each element. MathML renderers not supporting CSS may
ignore these attributes. MathML specifies these attribute values as general
strings, even if style sheet mechanisms have more restrictive syntaxes for
them. That is, any value for them is valid in MathML.
In order to facilitate compatibility with linking mechanisms, all
MathML elements accept the xlink:href
attribute.
All MathML elements also accept the xref
attribute for use in parallel markup (Section 5.3 [Parallel Markup]). The id is also used
in this context.
Every MathML element, because of a legacy from MathML 1.0, also
accepts the deprecated attribute
other (Section 7.2.3 [Attributes for unspecified data])
which was conceived for passing non-standard attributes without
violating the MathML DTD. MathML renderers are only required to
process this attribute if they respond to any attributes which are not
standard in MathML. However, the use of other
is strongly deprecated when there are already other ways within MathML
of passing specific information.
See also Section 3.2.2 [Mathematics style attributes common to token elements] for a list of MathML attributes which can be used on most presentation token elements.
MathML ignores whitespace occurring outside token elements. Non-whitespace characters are not allowed there. Whitespace occurring within the content of token elements is `trimmed' from the ends, i.e., all whitespace at the beginning and end of the content is removed. Whitespace internal to content of MathML elements is `collapsed' canonically, i.e., each sequence of 1 or more whitespace characters is replaced with one space character (sometimes called a blank character).
In MathML, as in XML, `whitespace' means simple spaces,
tabs, newlines, or carriage returns, i.e., characters with hexadecimal
Unicode codes U+0020, U+0009, U+000A, or
U+000D, respectively.
For example, <mo> ( </mo> is equivalent to
<mo>(</mo>, and
<mtext> Theorem 1: </mtext>
is equivalent to
<mtext>Theorem 1:</mtext>.
Authors wishing to encode whitespace characters at the start or end of
the content of a token, or in sequences other than a single space, without
having them ignored, must use or other
`whitespace' non-marking entities as described in Section 6.2.4 [Non-Marking Characters]. For example, compare
<mtext> Theorem 1: </mtext>
with
<mtext> Theorem 1: </mtext>
When the first example is rendered, there is no whitespace before `Theorem', one space between `Theorem' and `1:', and no whitespace after `1:'. In the second example, a single space is rendered before `Theorem', two spaces are rendered before `1:', and there is no whitespace after the `1:'.
Note that the xml:space attribute does not apply
in this situation since XML processors pass whitespace in tokens to a
MathML processor; it is the MathML processing rules which specify that
whitespace is trimmed and collapsed.
For whitespace occurring outside the content of the token elements mi, mn, mo, ms, mtext, ci, cn and annotation, an mspace element should be used, as opposed to an mtext element containing only `whitespace'
entities.
Overview: Mathematical Markup Language (MathML) Version 2.0
Previous: 1 Introduction
Next: 3 Presentation Markup