




Next: Example (from Program LA_GEEVX_EXAMPLE)
Up: Standard Nonsymmetric Eigenvalue Problems
Previous: Purpose
Contents
Index
- A
- (input/output) REAL or COMPLEX square array,
shape
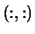 .
.
On entry, the matrix 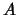 .
.
On exit, the contents of A are destroyed.
- w
- (output) REAL or COMPLEX array,
shape
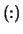 with
with  (w)
(w) 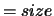 (A,1).
(A,1).
The computed eigenvalues.
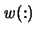 ::= WR(:), WI(:)
::= WR(:), WI(:)  W(:),
W(:),
where
WR(:), WI(:) are of REAL type
(for the real and imaginary parts)
and W(:) is of COMPLEX type.
Note: If 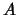 is real, then a complex-conjugate pair appear
consecutively, with the eigenvalue having the positive
imaginary part appearing first.
is real, then a complex-conjugate pair appear
consecutively, with the eigenvalue having the positive
imaginary part appearing first.
- VL
- Optional (output) REAL or COMPLEX
square array, shape
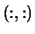 with
with 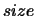 (VL,1)
(VL,1) 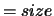 (A,1).
(A,1).
The left eigenvectors 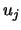 are stored in the
columns of VL in the order of their eigenvalues.
Each eigenvector is scaled so that the Euclidean norm is 1 and the
largest component is real.
are stored in the
columns of VL in the order of their eigenvalues.
Each eigenvector is scaled so that the Euclidean norm is 1 and the
largest component is real.
Note: If 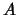 is real then complex eigenvectors,
like their eigenvalues,
occur in complex conjugate pairs. The real and imaginary
parts of the first eigenvector of the pair are stored in
VL
is real then complex eigenvectors,
like their eigenvalues,
occur in complex conjugate pairs. The real and imaginary
parts of the first eigenvector of the pair are stored in
VL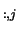 and VL
and VL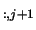 , respectively. Thus a
complex conjugate pair is given by
, respectively. Thus a
complex conjugate pair is given by
- VR
- Optional (output) REAL or COMPLEX
square array, shape
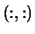 with
with 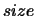 (VR,1)
(VR,1) 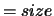 (A,1).
(A,1).
The right eigenvectors 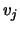 are stored in the
columns of VR in the order of their eigenvalues.
Each eigenvector is scaled so that the Euclidean norm is 1 and the
largest component is real.
are stored in the
columns of VR in the order of their eigenvalues.
Each eigenvector is scaled so that the Euclidean norm is 1 and the
largest component is real.
Note: If 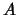 is real then complex eigenvectors,
like their eigenvalues,
occur in complex conjugate pairs. The real and imaginary
parts of the first eigenvector of the pair are stored in
VR
is real then complex eigenvectors,
like their eigenvalues,
occur in complex conjugate pairs. The real and imaginary
parts of the first eigenvector of the pair are stored in
VR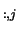 and VR
and VR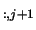 , respectively. Thus a
complex conjugate pair is given by
, respectively. Thus a
complex conjugate pair is given by
- BALANC
- Optional (input) CHARACTER(LEN=1).
Indicates whether the input matrix should be permuted and/or
diagonally scaled.
![\begin{optionarg}
\item[{$ =$\ 'N':}] Do not permute or scale;
\item[{$ =$\ 'P...
...ut do not permute;
\item[{$ =$\ 'B':}] Both permute and scale.
\end{optionarg}](img766.gif)
Default value: 'N'.
- ILO,IHI
- Optional (output) INTEGER.
ILO and IHI are determined when 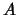 is
balanced. The balanced
is
balanced. The balanced 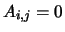 if
if 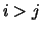 and
and
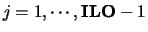 or
or
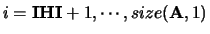 .
.
- SCALE
- Optional (output) REAL array,
shape
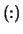 with
with 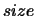 (SCALE)
(SCALE) 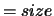 (A,1).
(A,1).
Details of the permutations and scaling factors applied
when balancing 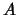 . If
. If 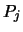 is the index of the row and column
interchanged with row and column
is the index of the row and column
interchanged with row and column 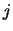 , and
, and 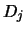 is the scaling
factor applied to row and column
is the scaling
factor applied to row and column 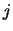 , then
, then
- ABNRM
- Optional (output) REAL.
The 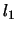 norm of the balanced matrix (the maximum
of the sum of absolute values of elements of any column).
norm of the balanced matrix (the maximum
of the sum of absolute values of elements of any column).
- RCONDE
- Optional (output) REAL array,
shape
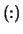 with
with 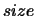 (RCONDE)
(RCONDE) 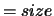 (A,1).
(A,1).
RCONDE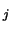 is the reciprocal condition number of the
is the reciprocal condition number of the 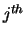 eigenvalue.
eigenvalue.
- RCONDV
- Optional (output) REAL array,
shape
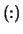 ,
, 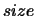 (RCONDV)
(RCONDV) 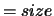 (A,1).
(A,1).
RCONDV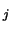 is the reciprocal condition number of the
is the reciprocal condition number of the 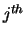 right eigenvector.
right eigenvector.
- INFO
- Optional (output) INTEGER.
![\begin{infoarg}
\item[{$=$\ 0:}] successful exit.
\item[{$<$\ 0:}] if {\bf INF...
...and $i+1:n$\ of {\it w}
contain eigenvalues which have converged.
\end{infoarg}](img775.gif)
If INFO is not present and an error occurs, then the program is
terminated with an error message.
References: [1] and [17,9,20].





Next: Example (from Program LA_GEEVX_EXAMPLE)
Up: Standard Nonsymmetric Eigenvalue Problems
Previous: Purpose
Contents
Index
Susan Blackford
2001-08-19
![\begin{optionarg}
\item[{$ =$\ 'N':}] Do not permute or scale;
\item[{$ =$\ 'P...
...ut do not permute;
\item[{$ =$\ 'B':}] Both permute and scale.
\end{optionarg}](img766.gif)
![\begin{infoarg}
\item[{$=$\ 0:}] successful exit.
\item[{$<$\ 0:}] if {\bf INF...
...and $i+1:n$\ of {\it w}
contain eigenvalues which have converged.
\end{infoarg}](img775.gif)